Принятие решений в условиях полной неопределенности

Неопределенность, связанную с отсутствием информации о вероятностях состоянии среды (природы), называют «безнадеж­ной» или «дурной».

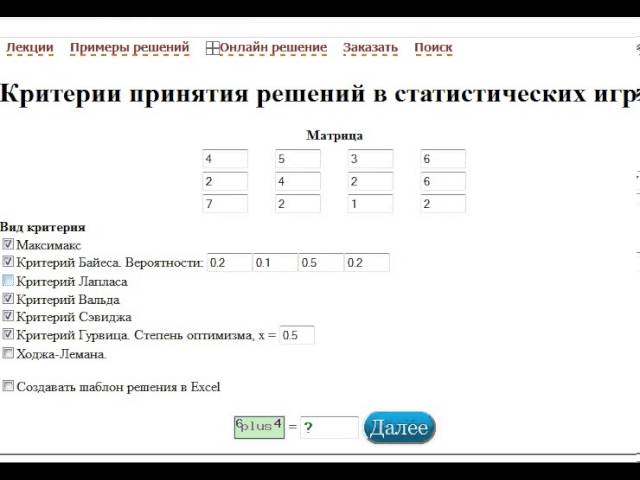
В таких случаях для определения наилучших решении ис­пользуются следующие критерии: максимакса, Вальда, Сэвиджа, Гурвица. Альтернативные подходы, в частности принципы Байеса - Лапласа, рассматриваются в разд. 6.2.1.

Применение каждого из перечисленных критериев проиллю­стрируем на примере матрицы выигрышей (3.1) или связанной с ней матрицы рисков (3.2).

Критерий максимакса. С его помощью определяется страте­гия, максимизирующая максимальные выигрыши для каждого состояния природы. Это критерий крайнего оптимизма. Наилуч­шим признается решение, при котором достигается максималь­ный выигрыш, равный .

Нетрудно увидеть, что для матрицы А наилучшим решением будет А₁ . при котором достигается максимальный выигрыш - 9.

Следует отметить, что ситуации, требующие применения такого критерия, в экономике в общем нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствовать­ся принципом «или пан, или пропал».

Максиминный критерий Вальда. С позиций данного крите­рия природа рассматривается как агрессивно настроенный и сознательно действующий противник типа тех, которые проти­водействуют в стратегических играх (см. гл. 2). Выбирается ре­шение, для которого достигается значение .

Для платежной матрицы А (3.1) нетрудно рассчитать:

• для первой стратегии ( i= 1) ;

• для второй стратегии ( i =2) ;

• для третьей стратегии ( i =3) .

Тогда . что соответствует второй стратегии A ₂ игрока 1.

В соответствии с критерием Вальда из всех самых неудач­ных результатов выбирается лучший (W = 3). Это перестрахо­вочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определя­ется отношением игрока к риску.

Критерий минимаксного риска Сэвиджа. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличи­ем, что игрок руководствуется не матрицей выигрышей А (3.1), а матрицей рисков R (3.2):

Для матрицы R (3.2) нетрудно рассчитать:

• для первой стратегии ( i =1) ;

• для третьей стратегии ( i =3) .

Минимально возможный из самых крупных рисков, равный 4, достигается при использовании первой стратегии А₁ .

Критерий пессимизма-оптимизма Гурвица. Этот критерий при выборе решения рекомендует руководствоваться некоторым сред­ним результатом, характеризующим состояние между крайним пес­симизмом и безудержным оптимизмом. Согласно этому критерию стратегия в матрице А выбирается в соответствии со значением

При p = 0 критерий Гурвица совпадает с максимаксным кри­терием, а при р = 1 - с критерием Вальда. Покажем процедуру применения данного критерия для матрицы А (3.1) при р = 0,5:

• для первой стратегии

• для второй стратегии

• для третьей стратегии

Тогда . т.е. оптимальной является вторая стратегия А₂ .

Применительно к матрице рисков R критерий пессимизма-оптимизма Гурвица имеет вид:

При р = 0 выбор стратегии игрока 1 осуществляется по ус­ловию наименьшего из всех возможных рисков ( ); при р = 1 - по критерию минимаксного риска Сэвиджа.

В случае, когда по принятому критерию рекомендуется к использованию несколько стратегий, выбор между ними может делаться по дополнительному критерию, например в расчет могут приниматься средние квадратичные отклонения от средних вы­игрышей при каждой стратегии. Данная идея отвечает подходу, рассмотренному в разд.1.2 (см. рис. 1.1). Еще раз подчеркнем, что здесь стандартного подхода нет. Выбор может зависеть от склонности к риску ЛПР.

В заключение приведем результаты применения рассмотрен­ных выше критериев на примере следующей матрицы выигры­шей:

Для игрока 1 лучшими являются стратегии:

Поскольку стратегия А₃ , фигурирует в качестве оптимальной по трем критериям выбора из четырех испытанных, степень ее надежности можно признать достаточно высокой для того, что­бы рекомендовать эту стратегию к практическому применению.

Таким образом, в случае отсутствия информации о вероят­ностях состоянии среды теория не дает однозначных и матема­тически строгих рекомендации по выбору критериев принятия решений. Это объясняется в большей мере не слабостью тео­рии, а неопределенностью самой ситуации. Единственный ра­зумный выход в подобных случаях - попытаться получить до­полнительную информацию, например, путем проведения ис­следований или экспериментов. В отсутствие дополнительной информации принимаемые решения теоретически недостаточ­но обоснованы и в значительной мере субъективны. Хотя при­менение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определен­ной степени является субъективным (вследствие произвольно­сти выбора критерия принятия решения), оно тем не менее создает некоторое упорядочение имеющихся в распоряжении ЛПР данных: задаются множество состояний природы, альтер­нативные решения, выигрыши и потери при различных сочета­ниях состояния «среда - решение». Такое упорядочение пред­ставлений о проблеме само по себе способствует повышению качества принимаемых решений.

Такие предприниматели готовы рисковать, в рисковой ситуации они
маневрируют ресурсами, способны очень быстро находить новых партнеров
bibliotekar.ru/biznes-41/29.htm

Максимакс - Большая Энциклопедия Нефти и Газа, статья, страница 1

Максимакс ( maximax) - критерий оптимизма - определяет альтернативу, которая максимизирует максимальный результат для каждой альтернативы.  [1]

Максимакс - критерий принятия решений, стремящийся к риску субъекта; в соответствии с ним выбор падает на вариант с наилучшим из наилучших исходов.  [2]

Критерий максимакса используют при выборе рисковых решений в условиях неопределенности, как правило, субъекты, склонные к риску, или рассматривающие возможные ситуации как оптимисты.  [3]

Критерий максимакса соответствует стремлению к риску со стороны лица, принимающего решения.  [4]

Правило максимакса ориентирует субъект хозяйствования на наиболее счастливый ход управляемого процесса.  [5]

В случае критерия максимакса мы выбираем в качестве оптимальной такую стратегия, для которой самый благоприятный случай дает самый большой выигрыш.  [6]

Если ос 1, критерий Гурвица называется максимакс. или критерий азартного игрока. При а 0 он называется максимин, или критерий пессимиста.  [7]

При использовании данного критерия, называемого также критерием максимакса. ЛПР ориентируется на то, что условия функционирования анализируемых систем будут для него наиболее благоприятными. Вследствие этого оптимальным решением является стратегия, приводящая к получению наибольшего значения критерия оптимальности в платежной матрице. Этот критерий целесообразно применять в тех случаях, когда имеется принципиальная возможность повлиять на функции противоположной стороны.  [8]

При прочих равных условиях может быть выбран другой критерий - максимакса. не только отражающий стремление получить максимально высокий результат, но и несущий угрозу значительных потерь. Вероятные потери определенным образом коррелируются со значимостью результата, для обеспечения которого идут на риск.  [9]

Из приведенной таблицы видно, что оптимальная альтернатива рискового решения в условиях неопределенности по критерию максимакса. находящаяся в затененном поле, соответствует 200 усл.  [10]

В стратегии обеспечения постоянного превосходства достигнутого потенциала над уровнем потребности могут использоваться главным образом модели максимакса.  [11]

В этом случае для поиска оптимальных стратегий используются наряду с принципом гарантированного результата и другие критерии, например Максимакса. Вальда, Сэвиджа, Гурвица, которые рассмотрим далее.  [12]

Если анкетирование проведено с помощью специальных тестов, учитывающих правдивость ответов ( в пределе детектор лжи), то к матрице В применяем критерий максимакса. С его помощью определяется стратегия, максимизирующая максимальные выигрыши для каждого состояния понимания миссии.  [13]

Анализ табл. 2 позволяет заключить, что согласно критерию Вальда следует принять крайне пессимистическую стратегию Sh а стратегия S3 является наиболее приемлемой как согласно критерию Гурвица, так и согласно критерию максимакса. Нетрудно заметить, что, имея значения f jmax о /, можно легко построить матрицу рисков и использовать критерий Сэвиджа или Гурвица.  [15]

Страницы:      1    2

Минимаксное решение

Решения, принимаемые в условиях неопределенности, занимают весомую часть всего множества решений, принимаемых менеджерами. Но, как правило, на практике решения, принимаемые в условиях полной неопределенности, не встречаются. Для принятия решений предприятие должно собрать необходимый дополнительный объем релевантной информации и проанализировать ситуацию, либо принять решение на основе суждений, интуиции, анализа накопленного опыта руководителя. Для принятия оптимальных решений необходимо использовать научный подход при использовании различных методов.

К правилам принятия решений, при которых не учитывается численное значение вероятных исходов, относятся рассмотренные ранее максимаксное и максиминное решение, а также минимаксное решение и критерий Гурвица.

Минимаксное решение - это решение, при котором минимизируются максимальные потери. Это наиболее осторожный подход к принятию решений и наиболее учитывающий все возможные риски.

Правило минимакса (минимаксное правило возможных потерь ) состоит в том, чтобы для каждого решения выбрать максимально возможные потери. Затем выбирается решение, которое ведет к минимальному значению максимальных потерь.

Под потерями учитываются не только реальные потери, но и упущенные возможности. При использовании данного правила внимание уделяется возможным потерям, чем доходам.

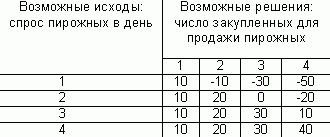
На основании данных предыдущего примера по реализации пирожных составим таблицу возможных потерь, которая дает представление о прибылях каждого исхода, потерянных в результате принятия неправильного решения (число закупленных единиц).

Таблица заполняется следующим образом.

Если количество закупленных пирожных равняется спросу за день, то возможные потери равняются нулю.

Если было принято решение приобрести, например, 1 пирожное, а спрос в этот день составил 2 штуки, то упущенная выгода составит 1*(60-50)=10 руб. Это и есть возможные потери. Для 2 штук пирожных, которые могли бы продать, сумма возможных потерь составляет 20 руб. для 3-х пирожных - 30 руб.

В тех случаях, когда закупленная единица не была реализована, она приносит убыток 1* (50-30)=20, это тоже возможные потери.

Для каждого решения выбирается максимальное число возможных потерь. Это числа 30, 20, 40, 60 и определяем из них минимальное 20. Данное значение соответствует решению о закупке 2 штук. Следовательно, руководствуясь правилом минимакса, минимальная величина максимальных потерь возникает в результате закупки двух пирожных в день.

Критерий Гурвица (Hurwicz criterion)- это компромиссный способ принятия решений.

При выборе решения из двух крайностей: пессимистической оценкой по критерию максимина и оптимистической оценкой максимакса рационально придерживаться промежуточной позиции, граница которой регулируется показателем пессимизма-оптимизма µ, называемым степенью оптимизма в критерии Гурвица.

В соответствии с этим компромиссным решением будет линейная комбинация минимального и максимального выигрыша

где 0 < µ < 1,

gnm - размер возможного дохода, который соответствует решениям при данных исходах.

Причем величину µ определяет исследователь или лицо, принимающее решение, при этом значению µ=1 критерию Гурвица соответствует правилу максимина (критерий Вальда), а значению µ =0 - правило максимакса (критерий Сэвиджа).

Критерий Гурвица заключается в том, что минимальному и максимальному результатам каждого решения присваивается "вес". Умножив результаты на соответствующие веса и суммируя их, лицо, принимающее решение, получает общий результат. Далее выбирается решение с наибольшим результатом.

Вернемся к предыдущему примеру и заполним таблицу по методу Гурвица.

Для четырех возможных решение были ранее получены максимаксное и максминное решения. Пусть вес минимального результата равен 0,4, следовательно, вес максимального - 0,6.

В данном примере критерий Гурвица свидетельствует в пользу решения о закупке одного пирожного, максимальная сумма составила 10. Очевидно, что при выборе других весов результат получается иным.

Поэтому к достоинству и одновременно недостатку критерия Гурвица относится необходимость присваивания весов возможным исходам: это позволяет учесть специфику ситуации, однако при этом всегда присутствует субъективный человеческий фактор - предпочтения аналитика.

Минимаксное решение. Критерий Гурвица

Критерии выбора решений в условиях полной неопределенности - Студопедия

Критерий максимакса (крайнего, «розового» оптимизма) основан на оптимистическом принципе Л. Гурвица, согласно которому выбирается вариант, обеспечивающий наибольший эффект в самой благоприятной ситуации.

Если матрицу последствий (3.1) рассматривать как матрицу эффекта Е, то эффективное решение выбирается из условий обеспечения максимума:

Данный критерий соответствует стратегии 1 (см. рис.3.6), его целесообразно применять в тех случаях, когда имеется возможность повлиять на противоположную сторону, чтобы сделать более благоприятной неконтролируемую внешнюю среду, и реализовать возможности оптимального использования управляемых внутренних факторов.

Пример 3.3. Принимая матрицу последствий в примере 3.2 за матрицу эффектов выбрать вариант решения по критерию максимакса.

1. Исходные данные вводятся в Excel (рис.3.9). Затем, используя функцию МАКС для ячеек (B4:F4;…; B7:F7), последовательно находятся максимальные значения по каждому решению . a₁ =8, a₂ =12, a₃ =10, a₄ =8 .

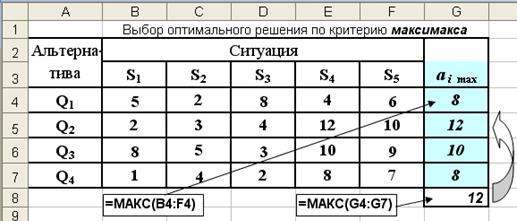
Рис. 3.9. Результаты выбора оптимального решения по критерию максимакса

2. Из последовательности найденных максимальных значений a_i (G4:G7) с помощью функции МАКС (ячейка G8) выбирается наибольшее значение: a₂ =12. с учетом этого рекомендуется принять второе решение.

Если элементами матрицы A (3.1) являются затраты З, то их можно рассматривать как потери и тогда решение обеспечивающее наименьшие затраты выбирается из условий минимизации затрат:

Критерий минимина (пессимизма)основан на пессимистическом принципе, согласно которому в условиях неблагоприятной внешней среды управляемые факторы могут быть использованы небла­гоприятным образом. Тогда, если матрица последствий является матрицей эффекта Е, то эффективное решение выбирается из условий обеспечения максимума:

В реальных условиях не всегда возможен контроль за неконтролируемыми факторами внешней среды, особенно когда необходимо учитывать фактор времени. Например, при долгосрочном прогнозировании и планировании; проектировании сложных объектов и др. Или например, издержки производства являются контролируемыми факторами на коротких интервалах времени и неконтролируемые в долгосрочной перспективе, поскольку заранее неизвестны стоимость электроэнергии, стоимость материалов и покупных изделий и т.п. Еще одним примером является определение объемов производства продукции предприятия (управляемый фактор), которые зависят от разных факторов связанных с процессом производства. Эти факторы относятся к внутренней среде предприятия: уровень конструкторской и технологической подготовки производства, тип используемого обо­рудования, квалификация работающих и пр.

Этому критерию соответствует стратегия 2 (см. рис.3.6).

Пример 3.4. Принимая матрицу последствий в примере 3.2 за матрицу эффектов выбрать вариант решения по критерию минимина.

1. Исходные данные вводятся в Excel (рис.3.10). Затем, используя функцию МИН для ячеек (B4:F4;…; B7:F7), последовательно находятся минимальные значения по каждому i -му решению . a₁ =2, a₂ =2, a₃ =3, a₄ =1 .

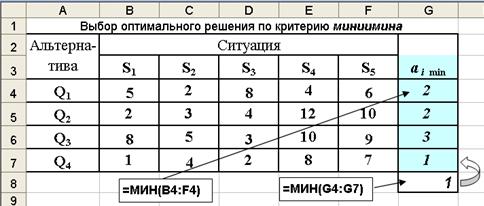
Рис. 3.10. Результаты выбора оптимального решения по критерию минимина

3. Из последовательности найденных минимальных значений a_i (G4:G7) с помощью функции МИН (ячейка G8) выбирается наименьшее значение: a₄ =1. с учетом этого рекомендуется принять четвертое решение.

При анализе матрицы затрат критерий пессимизма принимает следующий вид

Критерий максимина(крайнего пессимизма) основан на пессимистическом принципе А. Вальда, согласно которому выбирается тот вариант, результат которого оказывается самым благоприятным среди наименее благоприятных.

Если ожидаемая ситуация будет складываться неблагоприятно, т.е. принесет самый малый доход: a_i = min a_ij . то выбирается такое решение, для которого минимальный (гарантированный) доход окажется наибольшим

Данный критерий является консервативным, поскольку предлагает выбор с осторожной линией поведения, поэтому его целесообразно использовать в тех случаях, когда необходимо обеспечить успех при любых возможных условиях. В матрице решений (рис. 3.6) критерий Вальда соответствует стратегии 3.

Пример 3.5. Для матрицы последствий в примере 3.2 выбрать вариант решения по критерию максимина.

1. По каждому i –му альтернативному решению, используя функцию МИН находятся минимальные значения . a₁ =2, a₂ =2, a₃ =3, a₄ =1 (см. рис. 3.11, ячейки G4:G7)

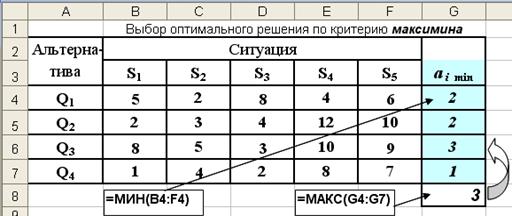
Рис. 3.11. Результаты выбора оптимального решения по критерию максимина

2. С помощью функции МАКС из последовательности найденных минимальных значений a_i (G4:G7) выбирается максимальное a₃ = 3 (ячейка G8).

3. Согласно правилу Вальда (3.11) предпочтение следует отдать третьему варианту решения (i=3 ), с максимально гарантированным результатом (выигрышем) независимо от варианта ситуации (внешних условий).

Критерий минимакса(минимаксного риска, ожидания убытков) основан на принципе разочарования Л. Сэвиджа. Согласно этому принципу, выбирается вариант, при реализации которого максимально возможное разочарование (разность между максимально возможным результатом и результатами, которые можно получить по каждому из оставшихся вариантов) оказывается наименьшим.

Здесь ориентируются на худшую ситуацию, которая сопряжена с наибольшим риском. При выборе решения используется матрица рисков R (3.5). Лучшим считается вариант решения, при котором максимальное значение риска будет наименьшим:

При принятии инвестиционных решений в условиях неопределенности с ориентацией на наихудшие исходы применяются пессимистический критерий (максимина) и критерий разочарования (минимакса).

Данный критерий используется в тех случаях, когда требуется в любых условиях избежать большого риска, он соответствует стратегии 4 (рис. 3.6).

Пример 3.6. По матрице последствий в примере 3.2 выбрать вариант решения по критерию минимакса.

1. Предварительно по матрице последствий примера 2, используя выражение (3.4), рассчитываются элементы матрицы риска рис. 3.12.

2. В каждой строке матрицы рисков с помощью функции МАКС выбирается ее максимальный элемент (ячейки G4:G7): r_i = . r₁ = 8, r₂ = 6, r₃ = 5, r₄ = 7.

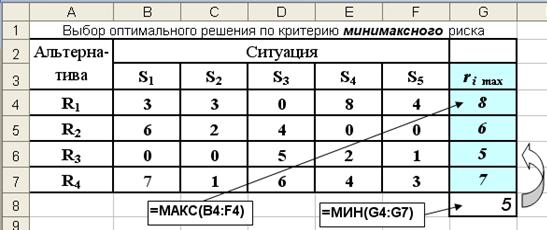
Рис. 3.12. Результаты выбора оптимального решения по критерию минимакса

3. Согласно правилу Сэвиджа из этих величин выбирается наименьшая (функция МИН в ячейке G8): r₃ = 5, т.е. следует принять 3-е решение (i=3 ). Выбор этого варианта означает, что максимальные потери при различных вариантах ситуации окажутся минимальными и не превысят 5 единиц.

Критерий Гурвица обобщенного максимина(пессимизма-оптимизма) предполагает выбор смешанной стратегии. когдав определенной пропорции сочетаются пессимизм (осторожность) и оптимизм (склонность к значительному риску), т.е. выбирается промежуточное решение между линией поведения в расчете на худшее и линией поведения в расчете на лучшее.

По данному критерию выбирается вариант решения, при котором достигается максимальный показатель G. определяемый из выражения:

где а_ij – выигрыш при i -м решении при j -м ва­рианте обстановки,

a – коэффициент, отражающий степень оптимизма (0 ≤ a ≤ 1 ): при a = 0 выбирается линия поведения в расчете на лучшее, т.е. делается ориентация на предельный риск (получаем максимаксный критерий); при a = 1 делается ориентация на худшее, тогда получаем критерий Вальда - ориентир на осторожное поведение. Промежуточные значения a между 0 и 1 и выбираются в зависимости от конкретной обстановки и склонности к риску лица, принимающего решение.

Пример.3.7. Предприятие готовится выпускать новые виды продукции, при этом возможны четыре варианта решений Q₁. Q₂ . Q₃ . Q₄ . каждому из которых соответствует определенный вид продукции или их сочетание. Структуру спроса на продукцию характеризуют три варианта обстановки S₁ . S₂ . S₃ . Эффективности выпуска новых видов продукции а_ij длякаждой парысочетаний решений Q_i (i=1,2,…,m ) и обстановке S_j (j=1,2,…,n ) приведены в таблице на рис.3.12. Необходимо по критерию Гурвица найти наиболее выгодное решение Q_i и оценить влияние коэффициента оптимизма на выбор решения.

1. Зададимся последовательностью коэффициентов k с шагом 0,25: 0; 0,25; 0,50; 0,75; 1,00 и введем исходные данные на рабочий лист Excel, рис. 3.12.

2. Результаты расчета показателя G по выражению (3.13) для различ­ных вариантов решений в зависимости от величины коэффици­ента k приведены в нижней таблице рис.3.13.

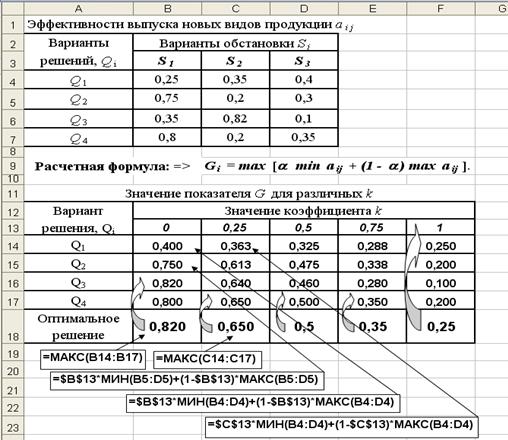
Рис. 3.13. Исходные данные, расчетные формулы и результаты расчета критерия Гурвица (стрелки показывают эффективные решения)

Как видно из рисунка (ячейки В18:F18), изменение коэффициента k влияет на выбор вари­анта решения, которому стоит отдать предпочтение.

Выбор того или иного критерия зависит от ряда факторов:

- характера решаемой задачи;

- склонности к риску лиц, принимающих решение.

Следует отметить, что рассмотренные способы и приемы решения задач в условиях риска и неопределенности не ограничиваются перечисленными методами. В зависимости от конкретной ситуации в процессе анализа могут использоваться и другие методы, например, использование среднеквадратического отклонения и коэффициента вариации как меры риска.

© studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам